How Many Tangents That Are Common to Both Circles Can Be Drawn?
Finding common tangents to two circles
Given two circles. It is required to find all their common tangents, i.e. all such lines that touch both circles simultaneously.
The described algorithm will also piece of work in the case when ane (or both) circles degenerate into points. Thus, this algorithm tin can besides exist used to discover tangents to a circle passing through a given point.
The number of common tangents
The number of common tangents to 2 circles tin can be 0,1,2,three,iv and infinite. Look at the images for different cases.
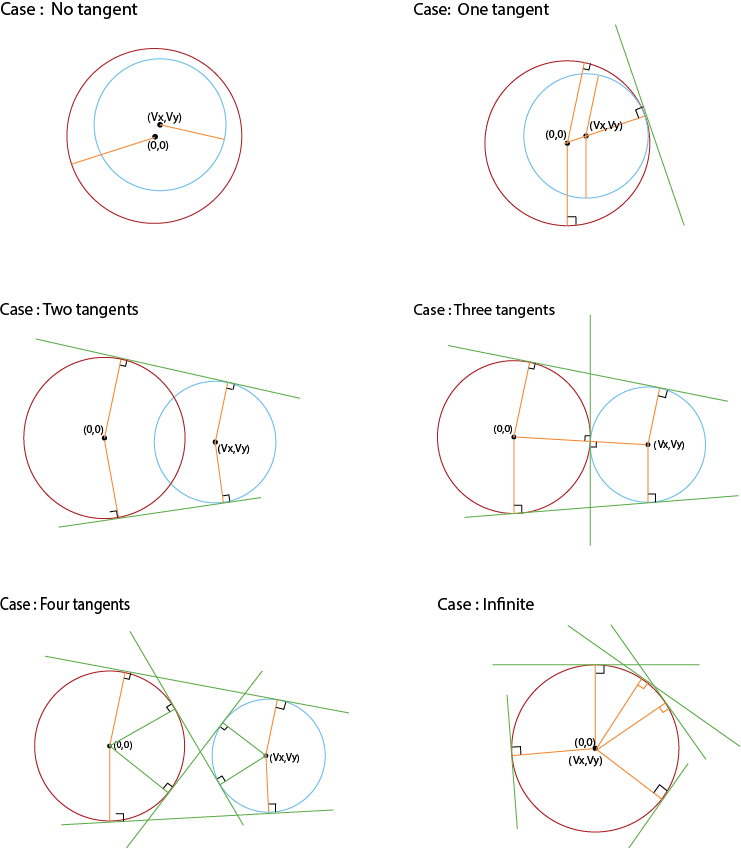
Hither, we won't be considering degenerate cases, i.east when the circles coincide (in this case they take infinitely many mutual tangents), or one circle lies inside the other (in this case they have no common tangents, or if the circles are tangent, there is one common tangent).
In virtually cases, two circles have four common tangents.
If the circles are tangent , then they volition have 3 common tangents, only this tin be understood as a degenerate example: equally if the two tangents coincided.
Moreover, the algorithm described below will work in the example when one or both circles have zippo radius: in this case there will be, respectively, two or 1 common tangent.
Summing up, we will always wait for iv tangents for all cases except infinite tangents case (The space tangents case needs to exist handled separately and information technology is not discussed hither). In degenerate cases, some of tangents volition coincide, but even so, these cases will also fit into the large motion-picture show.
Algorithm
For the sake of simplicity of the algorithm, we will presume, without losing generality, that the center of the showtime circle has coordinates \((0, 0)\). (If this is not the case, then this tin exist achieved by just shifting the whole picture, and subsequently finding a solution, by shifting the obtained directly lines back.)
Denote \(r_1\) and \(r_2\) the radii of the first and second circles, and past \((v_x,v_y)\) the coordinates of the center of the 2d circle and point \(5\) different from origin. (Notation: we are not because the case in which both the circles are same).
To solve the trouble, we approach information technology purely algebraically . We demand to detect all the lines of the form \(ax + past + c = 0\) that lie at a altitude \(r_1\) from the origin of coordinates, and at a distance \(r_2\) from a signal \(5\). In improver, nosotros impose the condition of normalization of the directly line: the sum of the squares of the coefficients and must exist equal to i (this is necessary, otherwise the aforementioned straight line will correspond to infinitely many representations of the form \(ax + by + c = 0\)). Full we get such a system of equations for the desired \(a, b, c\):
\[\begin{align} a^2 + b^2 &= ane \\ \mid a \cdot 0 + b \cdot 0 + c \mid &= r_1 \\ \mid a \cdot v_x + b \cdot v_y + c \mid &= r_2 \end{marshal}\]
To go rid of the modulus, note that at that place are only four ways to open the modulus in this system. All these methods tin be considered past the general example, if we understand the opening of the modulus as the fact that the coefficient on the right-manus side may be multiplied by -ane. In other words, we plow to this system:
\[\begin{marshal} a^ii + b^ii &= 1 \\ c &= \pm r_1 \\ a \cdot v_x + b \cdot v_y + c &= \pm r_2 \cease{align}\]
Inbound the annotation \(d_1 = \pm r_1\) and \(d_2 = \pm r_2\) , we come to the conclusion that the system must have four solutions:
\[\brainstorm{align} a^2 + b^two &= 1 \\ c &= d_1 \\ a \cdot v_x + b \cdot v_y + c &= d_2 \cease{align}\]
The solution of this system is reduced to solving a quadratic equation. We will omit all the cumbersome calculations, and immediately give a ready respond:
\[\begin{marshal} a &= {( d_2 - d_1 ) v_x \pm v_y \sqrt{v_x^2 + v_y^2-(d_2-d_1)^two} \over {v_x^2 + v_y^ii} } \\ b &= {( d_2 - d_1 ) v_y \pm v_x \sqrt{v_x^two + v_y^2-(d_2-d_1)^2} \over {v_x^2 + v_y^2} } \\ c &= d_1 \cease{marshal}\]
Full we got eight solutions instead four. All the same, it is easy to empathise where superfluous decisions ascend: in fact, in the latter system, information technology is plenty to have only one solution (for example, the beginning). In fact, the geometric meaning of what we have \(\pm r_1\) and \(\pm r_2\) is articulate: we are actually sorting out which side of each circumvolve in that location is a straight line. Therefore, the two methods that arise when solving the latter system are redundant: information technology is enough to choose 1 of the two solutions (only, of course, in all 4 cases, yous must cull the aforementioned family of solutions).
The last matter that we have non still considered is how to shift the straight lines in the case when the first circumvolve was not originally located at the origin. However, everything is simple here: information technology follows from the linearity of the equation of a direct line that the value \(a \cdot x_0 + b \cdot y_0\) (where \(x_0\) and \(y_0\) are the coordinates of the original center of the first circle) must be subtracted from the coefficient \(c\).
Implementation
Nosotros first describe all the necessary data structures and other auxiliary definitions:
struct pt { double x, y; pt operator- (pt p) { pt res = { x-p.x, y-p.y }; return res; } }; struct circle : pt { double r; }; struct line { double a, b, c; }; const double EPS = 1E-9; double sqr (double a) { return a * a; } void tangents (pt c, double r1, double r2, vector<line> & ans) { double r = r2 - r1; double z = sqr(c.x) + sqr(c.y); double d = z - sqr(r); if (d < -EPS) render; d = sqrt (abs (d)); line fifty; l.a = (c.x * r + c.y * d) / z; l.b = (c.y * r - c.x * d) / z; l.c = r1; ans.push_back (fifty); } vector<line> tangents (circle a, circle b) { vector<line> ans; for (int i=-1; i<=1; i+=2) for (int j=-ane; j<=one; j+=2) tangents (b-a, a.r*i, b.r*j, ans); for (size_t i=0; i<ans.size(); ++i) ans[i].c -= ans[i].a * a.10 + ans[i].b * a.y; return ans; } Problems
TIMUS 1163 Chapaev
Source: https://cp-algorithms.com/geometry/tangents-to-two-circles.html
0 Response to "How Many Tangents That Are Common to Both Circles Can Be Drawn?"
Post a Comment